Chuỗi lũy thừa bắt nguồn từ khai triển Taylor của một hàm khả vi vô hạn

có dạng
 .
. 
Các câu hỏi sau cần được quan tâm:
+ Khi nào chuỗi (1) hội tụ? Nói rõ hơn ngoài  chuỗi (1) còn hội tụ tại những điểm
chuỗi (1) còn hội tụ tại những điểm  nào khác?
nào khác?
+ Trừ  ra, nếu chuỗi (1) hội tụ thì nó hội tụ đến đâu? Liệu giới hạn đó có phải
ra, nếu chuỗi (1) hội tụ thì nó hội tụ đến đâu? Liệu giới hạn đó có phải  ?
?
Để trả lời câu hỏi đầu, ta quan sát chuỗi lũy thừa một cách độc lập, chưa phải là chuỗi Taylor của hàm nào,
 .
.
Câu hỏi đầu tiên được trả lời qua hai ý sau:
+ (Định lý Abel) Có một số thực không âm  để
để
– khi  chuỗi (2) hội tụ,
chuỗi (2) hội tụ,
– khi  chuỗi (2) phân kỳ.
chuỗi (2) phân kỳ.
Tại hai đầu mút nói chung ta không biết chuỗi có hội tụ không. Chẳng hạn chuỗi  có bán kính hội tụ
có bán kính hội tụ  , hội tụ tại
, hội tụ tại  và phân kỳ tại
và phân kỳ tại  .
.
Vấn đề tại mút các bạn có thể tham khảo thêm ở bài
http://bomongiaitich.wordpress.com/2011/04/29/d%E1%BB%8Bnh-ly-abel-d%E1%BB%8Bnh-ly-tauber/
+ Từ ý trên ta có khái niệm bán kính hội tụ. Vậy bán kính hội tụ được tính như nào?
Bán kính hội tụ được tính nhờ công thức Cauchy-Hardamard
– hoặc  với
với  ,
,
– hoặc  với
với  .
.
Lưu ý rằng hai giới hạn trên chưa chắc tồn tại, tuy nhiên vẫn có bán kính hội tụ. Lúc đó bán kính được tính nhờ công thức
 với
với  .
.
Các bạn có thể thấy điều này qua ví dụ

có bán kính của chuỗi (2) là  .
.
Bán kính cũng có thể bằng  , chẳng hạn khi
, chẳng hạn khi  .
.
Bán kính cũng có thể bằng  , chẳng hạn khi
, chẳng hạn khi  .
.
Khi bán kính hội tụ  thì chuỗi (2) hội tụ đều trên
thì chuỗi (2) hội tụ đều trên ![[-r, r] [-r, r]](https://s0.wp.com/latex.php?latex=%5B-r%2C+r%5D&bg=ffffff&fg=4b5d67&s=0) với bất kỳ
với bất kỳ  .
.
Chuỗi gồm các số hạng là đạo hàm của từng số hạng của chuỗi (2)

cũng có bán kính hội tụ chính là bán kính hội tụ của chuỗi (2) vì
 .
.
Khi đó chuỗi các đạo hàm cũng hội tụ đều trên ![[-r, r] [-r, r]](https://s0.wp.com/latex.php?latex=%5B-r%2C+r%5D&bg=ffffff&fg=4b5d67&s=0) với bất kỳ
với bất kỳ  . Do đó chuỗi các đạo hàm hội tụ đến đạo hàm của chuỗi (2) tại mọi điểm trong
. Do đó chuỗi các đạo hàm hội tụ đến đạo hàm của chuỗi (2) tại mọi điểm trong  . Chuỗi (2) hội tụ đến hàm
. Chuỗi (2) hội tụ đến hàm  khả vi trên
khả vi trên  .
.
Bằng quy nạp sẽ dẫn đến chuỗi (2) hội tụ đến hàm  khả vi vô hạn trên
khả vi vô hạn trên  . Đạo hàm cấp
. Đạo hàm cấp  , của
, của  chính là hàm giới hạn của chuỗi gồm các số hạng là đạo hàm cấp
chính là hàm giới hạn của chuỗi gồm các số hạng là đạo hàm cấp  của số hạng tương ứng trong chuỗi (2). Từ đó có chuỗi (2) là khai triển Taylor của hàm
của số hạng tương ứng trong chuỗi (2). Từ đó có chuỗi (2) là khai triển Taylor của hàm  .
.
Giờ ta chuyển sang câu hỏi thứ hai, nghĩa là lúc này chuỗi (2) sinh ra từ việc khai triển Taylor của một hàm khả vi vô hạn 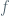 và
và
 .
.
Câu hỏi thứ hai trở thành, khi bán kính hội tụ  phải chăng
phải chăng
 với
với  ?
?
Câu hỏi này mới nghe có vẻ không cần thiết lắm nhưng các ví dụ sau chỉ ra sự cần thiết.
Ví dụ 1: Hàm  xác định bởi
xác định bởi
 khi
khi 
 khi
khi 
là hàm khả vi vô hạn và đạo hàm mọi cấp của nó tại  đều có giá trị bằng
đều có giá trị bằng  .
.
Ví dụ 2: Hàm  xác định bởi
xác định bởi
 khi
khi 
 khi
khi 
là hàm khả vi vô hạn và đạo hàm mọi cấp của nó tại  đều có giá trị bằng
đều có giá trị bằng  .
.
Hai ví dụ trên đều có chuỗi Taylor tại  đồng nhất
đồng nhất  . Nói cách khác hàm
. Nói cách khác hàm  và các tổ hợp tuyến tính của chúng là các hàm khác nhau nhưng có cùng chuỗi Taylor tại
và các tổ hợp tuyến tính của chúng là các hàm khác nhau nhưng có cùng chuỗi Taylor tại  .
.
Hơn nữa, nếu một hàm 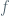 có chuỗi Taylor hội tụ đến chính nó thì tổng của
có chuỗi Taylor hội tụ đến chính nó thì tổng của 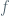 và bất kỳ hàm nào trong các hàm
và bất kỳ hàm nào trong các hàm  hay tổ hợp tuyến tính của hai hàm này có cùng chuỗi Taylor với hàm
hay tổ hợp tuyến tính của hai hàm này có cùng chuỗi Taylor với hàm 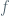 . Khi đó nếu ta chỉ biết chuỗi Taylor của
. Khi đó nếu ta chỉ biết chuỗi Taylor của 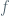 thì ta chưa biết nhiều về
thì ta chưa biết nhiều về 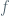 .
.
Vậy điều kiện gì để đảm bảo  khi
khi  ?
?
Trong cuốn “Giáo trình giải tích tập 2″ của các thầy Trần Đức long, Nguyễn Đình Sang, Hoàng Quốc Toàn đưa ra hai cách sau:
+(Điều kiện cần và đủ – đơn giản nhưng khó kiểm tra)
 với
với  ,
,
trong đó  .
.
+(Điều kiện đủ – Điều kiện bị chặn đều)
Có số dương  để
để
 .
.
Chứng minh điều kiện này ta dùng điều kiện trên với cách viết của Lagrange cho phần dư
 với
với  .
.
Có thể thấy điều kiện này cho ta thấy ngay chuỗi Taylor của các hàm  hội tụ đến chính các hàm này trên toàn đường thẳng.
hội tụ đến chính các hàm này trên toàn đường thẳng.
Ta có thể dùng điều kiện này kiểm tra sự hội tụ của chuỗi Taylor của hàm  tại từng điểm
tại từng điểm  , nhưng không nên dùng bán kính hội tụ vì
, nhưng không nên dùng bán kính hội tụ vì  , mà chỉ xét trên tập
, mà chỉ xét trên tập  đủ lớn để chứa
đủ lớn để chứa  .
.
Ta cũng có thể làm tốt hơn, nghĩa là giảm nhẹ điều kiện trên
Có số dương  để
để
 .
.
Nếu viết phần dư dưới dạng tích phân

thì ta có thể có điều kiện khác như sau.
Đạo hàm mọi cấp của hàm 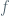 đều không âm trên
đều không âm trên  .
.
(Bài 3.4.15 trong “Problems in Mathematical analysis II” của W.J. Kaczor – M.T. Nowak)
Với việc dùng điều kiện này dễ dàng có ngay chuỗi Taylor của hàm  hội tụ đến chính hàm này.
hội tụ đến chính hàm này.
Câu hỏi: liệu có thể thay điều kiện không âm bởi điều kiện không đổi dấu?
Ngoài ra còn vài câu hỏi khác chẳng hạn:
– câu hỏi về chuỗi Taylor của tổng hai hàm khả vi vô hạn, tích của hai hàm khả vi vô hạn và (khó hơn) hợp thành của hai hàm khả vi vô hạn?
Với câu hỏi về tổng và tích ta dùng Điều kiện cần và đủ trong sách “Giáo trình giải tích tập 2″.
Với câu hỏi về hợp thành các bạn tham khảo các bài 3.4.16, 17, 18, 19 trong cuốn “Problems in mathematical analysis II”.
Đến lúc ta chuyển sự quan tâm sang chuỗi Fourier, một cách nhìn từ hàm phức: chuỗi lũy thừa tại điểm mút!
Ta cũng thử đi giống như chuỗi lũy thừa, nghĩa là ban đầu ta quan tâm chuỗi Fourier một cách độc lập
 .
. 
Tuy nhiên khác với chuỗi lũy thừa có bán kính hội tụ, chuỗi Fourier không có bán kính hội tụ! Nói cách khác ta không xem với  nào thì chuỗi hội tụ như kiểu chuỗi lũy thừa vì làm điều này khá khó! Giờ ta lại quan tâm đến các hệ số
nào thì chuỗi hội tụ như kiểu chuỗi lũy thừa vì làm điều này khá khó! Giờ ta lại quan tâm đến các hệ số  .
.
Dùng Weierstrass có thể thấy ngay nếu

thì chuỗi (3) hội tụ đều đến một hàm  liên tục, tuần hoàn chu kỳ
liên tục, tuần hoàn chu kỳ  .
.
Một số chuỗi chẳng hạn

có thể dễ dàng kiểm tra bởi điều kiện trên.
Tuy nhiên ta cũng biết chuỗi

hội tụ
mặc dù chuỗi

phân kỳ.
Chú ý thêm chuỗi

hội tụ đến  khi
khi 
(xem bài
http://bomongiaitich.wordpress.com/2012/05/08/ham-phuc-moi-lien-he-giua-chuoi-fourier-va-chuoi-luy-thua/).
Thác triển lẻ, tuần hoàn chu kỳ  ta được hàm không liên tục tại
ta được hàm không liên tục tại  .
.
Tiếp tục chuỗi Fourier-sine ta có một số kết quả thú vị sau.
Bài 2.5.56, 57 (trong “Problems in mathematical analysis III”).
Cho dãy  là dãy đơn điệu, hội tụ về
là dãy đơn điệu, hội tụ về  . Chuỗi Fourier-sine
. Chuỗi Fourier-sine

hội tụ đến hàm liên tục khi và chỉ khi
 .
.
Chú ý: Nếu chỉ quan tâm đến hội tụ thì dùng Định lý Dirichlet ta không cần điều kiện  .
.
Bài 2.5.58 (trong “Problems in mathematical analysis III”).
Cho dãy  là dãy đơn điệu, hội tụ về
là dãy đơn điệu, hội tụ về  . Chuỗi Fourier-sine
. Chuỗi Fourier-sine

hội tụ đến hàm bị chặn khi và chỉ khi
 (nghĩa là có số
(nghĩa là có số  để
để  ).
).
Phần còn lại là gì? Có vài ví dụ thực sự bất ngờ, rất khác so với chuỗi lũy thừa. Như đã biết ở trên khi đã hội tụ thì chuỗi lũy thừa sẽ hội tụ đến một hàm khả vi vô hạn nhận nó là khai triển Taylor.
Các chuỗi

(Problem 1/trang 95 trong “Fourier analysis: An introduction” của E.M. Stein – R. Shakarchi)
hay chuỗi

(Bài 2.5.22, 23 trong “Problems in mathematical analysis III”, ví dụ của P. Fatou)
mặc dù đều hội tụ, nhưng chúng đều không là khai triển Fourier của bất kỳ hàm khả tích (Lebesgue) trên ![[-\pi, \pi] [-\pi, \pi]](https://s0.wp.com/latex.php?latex=%5B-%5Cpi%2C+%5Cpi%5D&bg=ffffff&fg=4b5d67&s=0) .
.
Bài 2.5.59 trong “Problems in mathematical analysis” lại cho thấy với chuỗi Fourier-cosine có đôi chút khác như sau.
Nếu dãy  là dãy giảm về
là dãy giảm về  và có tính lồi, nghĩa là
và có tính lồi, nghĩa là

thì có hàm không âm, khả tích trên ![[-\pi, \pi] [-\pi, \pi]](https://s0.wp.com/latex.php?latex=%5B-%5Cpi%2C+%5Cpi%5D&bg=ffffff&fg=4b5d67&s=0) có khai triển Fourier
có khai triển Fourier
 .
.
Trong trường hợp  thì, theo Parseval, các chuỗi
thì, theo Parseval, các chuỗi

và các chuỗi

đều không là chuỗi Fourier của bất kỳ hàm bình phương khả tích trên ![[-\pi, \pi] [-\pi, \pi]](https://s0.wp.com/latex.php?latex=%5B-%5Cpi%2C+%5Cpi%5D&bg=ffffff&fg=4b5d67&s=0) nào, nói riêng bất kỳ hàm liên tục trên
nào, nói riêng bất kỳ hàm liên tục trên ![[-\pi, \pi] [-\pi, \pi]](https://s0.wp.com/latex.php?latex=%5B-%5Cpi%2C+%5Cpi%5D&bg=ffffff&fg=4b5d67&s=0) nào.
nào.
Sự bất ngờ ở chuỗi Fourier-sine ở trên dường như cho thấy cách tiếp cận chuỗi Fourier độc lập với khai triển Fourier của hàm số có gì đó không ổn? Có lẽ chỉ nên quan sát sự hội tụ của chuỗi Fourier sinh ra từ khai triển Fourier của một hàm đủ tốt?
Trong sách “Giáo trình giải tích II” có đưa ra lớp hàm “khả vi từng khúc”. Có thể thấy sự xuất hiện của lớp hàm này qua việc thác triển tuần hoàn chu kỳ  của hàm khả vi liên tục trên
của hàm khả vi liên tục trên  . Với
. Với  là hàm tuần hoàn chu kỳ
là hàm tuần hoàn chu kỳ  , khả vi từng khúc thì chuỗi Fourier
, khả vi từng khúc thì chuỗi Fourier

với 

 ,
,
hội tụ đến  ,
,
với  là giới hạn trái, giới hạn phải của
là giới hạn trái, giới hạn phải của 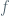 tại
tại  .
.
Nếu thêm điều kiện  liên tục tại
liên tục tại  thì chuỗi Fourier sẽ hội tụ đến
thì chuỗi Fourier sẽ hội tụ đến  .
.
Nhưng tại sao lại cần đến tính “khả vi từng khúc” trong khi cứ có hàm liên tục tuần hoàn chu kỳ  là có chuỗi Fourier!
là có chuỗi Fourier!
Khi đưa ra chuỗi Fourier vào năm 1807 trong công trình “Mémoire sur la propagation de la chaleur dans les corps solides” bản thân J. Fourier cũng đơn giản cho rằng chuỗi Fourier của hàm liên tục sẽ hội tụ. Phải đến năm 1873 Paul du Bois Reymond mới đưa ra ví dụ một hàm liên tục có chuỗi Fourier phân kỳ tại một vài điểm.
Một câu hỏi lại được đặt ra, liệu có cách nào khác để từ các hệ số Fourier của một hàm liên tục, tuần hoàn chu kỳ  “khôi phục” lại được hàm liên tục đó?
“khôi phục” lại được hàm liên tục đó?
Năm 1900, khi đó mới 20 tuổi, L. Fejér có câu trả lời khẳng định cho câu hỏi trên như sau:
Tổng Cesaro

hội tụ đều đến hàm tuần hoàn chu kỳ  , liên tục
, liên tục 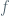 trên
trên ![[-\pi, \pi] [-\pi, \pi]](https://s0.wp.com/latex.php?latex=%5B-%5Cpi%2C+%5Cpi%5D&bg=ffffff&fg=4b5d67&s=0) .
.
(Bạn đọc có thể xem
http://en.wikipedia.org/wiki/Fej%C3%A9r%27s_theorem)
Từ kết quả trên của L. Fejer, U. Dini đưa ra cách kiểm tra nhẹ hơn điều kiện khả vi từng khúc như sau:
nếu hàm tuần hoàn chu kỳ  , khả tích
, khả tích  thỏa mãn
thỏa mãn

với  là hằng số
là hằng số
thì chuỗi Fourier sẽ hội tụ đến đúng  .
.
Trong trường hợp f khả vi từng khúc thì
 .
.
Từ điều kiện Dini cũng thấy được thêm vài ý sau.
+ Nếu 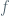 là hàm tuần hoàn chu kỳ
là hàm tuần hoàn chu kỳ  và
và
hoặc Lipschitz, nghĩa là có số dương  để
để
 ,
,
hoặc Holder cấp  , nghĩa là có số dương
, nghĩa là có số dương  để
để
 ,
,
thì chuỗi Fourier hội tụ đến đúng  .
.
+ (Mở rộng kết quả trong sách “Giáo trình giải tích II”) Nếu hàm 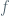 tuần hoàn chu kỳ
tuần hoàn chu kỳ  là hàm có biến phân bị chặn trong
là hàm có biến phân bị chặn trong ![[-\pi, \pi] [-\pi, \pi]](https://s0.wp.com/latex.php?latex=%5B-%5Cpi%2C+%5Cpi%5D&bg=ffffff&fg=4b5d67&s=0) , nghĩa là
, nghĩa là
có một số dương  để với bất kỳ phân hoạch
để với bất kỳ phân hoạch 

thì chuỗi Fourier hội tụ đến  .
.
Ta quay trở lại câu hỏi thứ hai, như của chuỗi lũy thừa, cho chuỗi Fourier:
Khi chuỗi Fourier của một hàm hội tụ thì nào có hội tụ đến chính hàm đó hay không?
Câu trả lời nằm ngay trong các kết quả ở trên. Kết quả đó lại cho thấy sự khác nhau về chất giữa chuỗi lũy thừa và chuỗi Fourier.
.
.
đủ tốt, cụ thể:
hội tụ.
xét hàm
xác định bởi
khi
,
lên toàn trục số, nghĩa là
khi
,
.
,
,
.
hội tụ đến đúng
khi
. (Tại hai đầu mút
thì sao?)
ra vô cùng.
hội tụ nên
khi
,
,
trên
lần lượt đến các tích phân
,
.
có
,
,
.
.
có
.
,
,
.
khi
,
làm sao lại chuyển sang
, hay tại sao
,
,
khi
?
đều có
với mọi số dương
. Khi đó,
với mọi
. Như vậy
hội tụ điểm đến
khi
. (Thực ra việc chứng minh này cũng dẫn đến sự hội tụ này là hội tụ đều trên từng compact.)
tại những điểm
khả vi phải và khả vi trái.
xét
.
nên
hội tụ tuyệt đối đều theo
trên
.
(đặt
),
.
.
.
có các điều sau.
mà hàm
khả vi phải và khả vi trái thì các hàm
,
.
.
nên
hội tụ.
đơn điệu giảm về
nên theo Dirichlet
hội tụ.
cố định bất kỳ. Khi đó có
để
.
liên tục trên
để với mọi
.
.
hội tụ nên
(đặt
).
.
là hàm liên tục, trơn từng khúc (có đạo hàm phải và trái tại mọi nơi), và khả tích tuyệt đối trên toàn đường thẳng, ta có
.
liên tục, trơn từng khúc và khả tích tuyệt đối
.
,
.
